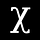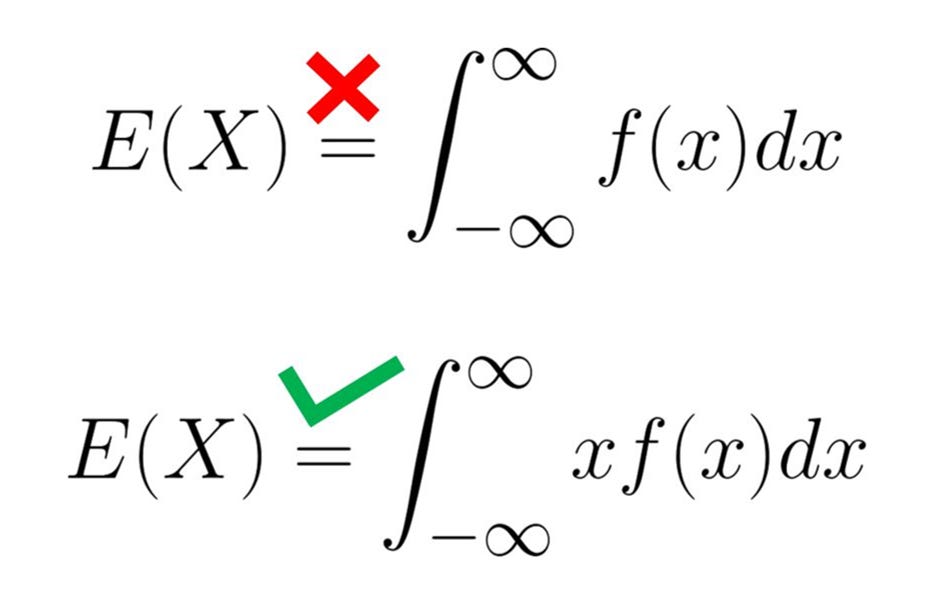A common mistake about expected values in mathematical statistics

A reminder about the integrand in the definition of expectation

In mathematical statistics, one of my most common mistakes occurs when I obtain the expected value of a random variable. It tends to happen more often when the random variable, 𝒳, is continuous. Here is my mistake:

Instead of using 𝓍⋅f(𝓍) as the integrand, I use only f(𝓍).

This may be trivial to remember. However, if the probability density function, f(𝓍), is very long and complicated, then I sometimes forget that I need to multiply an "𝓍" to that f(𝓍).

Here is one way to know if I have done something wrong:

If f(𝓍) is a legitimate probability density function (PDF), then integrating f(𝓍) over all real numbers should equal to 1. This is a basic property of PDFs.

Is it possible for the expectation to equal to 1? Yes. However, in my experience, it is more likely that I made a mistake and miswrote the integrand. This result generates an alarm bell for me, reminding me to check that I set up the integral properly.