Correcting a common mistake about linear regression

The response variable is normally distributed when conditioned on the covariate.

True or False:

In linear regression, the response variable, Y, is assumed to have a normal distribution.

That sentence sounds right, but it is actually not (completely) correct. What is wrong with it?

First, let’s review the model statement for simple linear regression.

\(Y_i = \beta_0 + \beta_1x_i + \varepsilon_i\)

\(\varepsilon_i \sim \text{Normal}(0, \sigma^2)\)

\(i = 1, 2, \dots, n\)

Note that Yᵢ is a linear combination of εᵢ; since εᵢ has a normal distribution, it is tempting to say that Yᵢ also has a normal distribution - but that is not true.

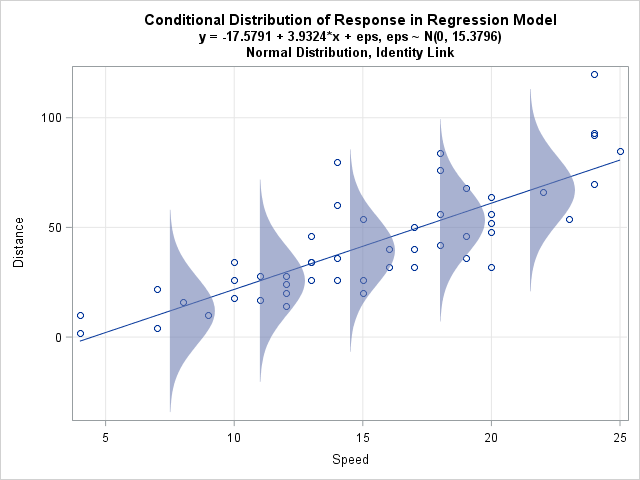
Yᵢ has a normal distribution for a given value of the covariate xᵢ. Thus, if you take all the values of Yᵢ at xᵢ = 7, their histogram or kernel density estimate would show a normal bell curve. (It is common among statisticians to say that the conditional distribution of Y for a given value of X is normal.)

To visualize this, I encourage you to view the plot below, which comes from an excellent blog post by Rick Wicklin, a distinguished researcher in computational statistics at SAS and a principal developer of SAS/IML software.

However, if you plot the histogram of all the Y values together, that will (likely) not be normally distributed. In statistical parlance, this is the marginal distribution of Y.

To summarize, the original statement at the beginning of this article is false. The correct statement is:

In linear regression, the response variable, Y, is assumed to have a normal distribution for a given value of the covariate x.