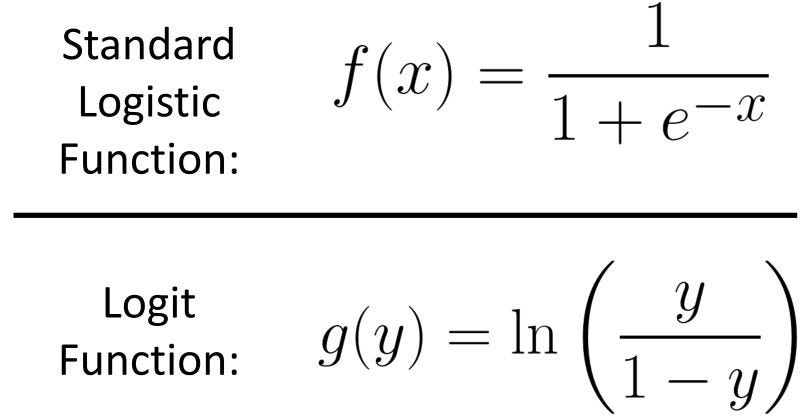Logistic Function โ Logit Function
Many people use "logistic" and "logit" interchangeably in the context of ๐ง๐๐๐ง๐๐จ๐จ๐๐ค๐ฃ ๐ข๐ค๐๐๐ก๐จ, but they actually have different meanings in the context of ๐๐ช๐ฃ๐๐ฉ๐๐ค๐ฃ๐จ.
Many people use the terms "logistic regression" and "logit regression" interchangeably. The Encyclopedia of Mathematics lists both terms in its "Statprob" category, but "logit regression" simply re-directs to "logistic regression".
However, the logistic function and the logit function are 2 different concepts. In fact, the logit function is the inverse of the standard logistic function.
As I always preach, it is best to use one term to denote one and only one concept. Thus, I encourage statisticians, data scientists, data analysts, economists, and practitioners in adjacent fields to use "logistic regression" and avoid "logit regression".
Addendum: As several LinkedIn commenters have correctly added, the term "logit regression" stems from the role that the logit function plays in logistic regression - it is the canonical link function between the expected value of the response variable and the linear predictor in this particular generalized linear model.
While I acknowledge the logic of this nomenclature, I still discourage using "logit regression" and urge you to use only "logistic regression". I remain steadfast in upholding clarity as the supreme goal when communicating mathematical concepts. Overwhelmingly, "logistic regression" is the most common term in statistics discourse, so we should use this term and avoid "logit regression".
If you are reading my posts for the first time: I'm Eric Cai, a statistician based in Toronto, Canada. I write about statistics, communication, and career development for professionals in data & analytics. Subscribe to get my articles delivered to your inbox at 9:30 AM Eastern time on Monday to Friday.