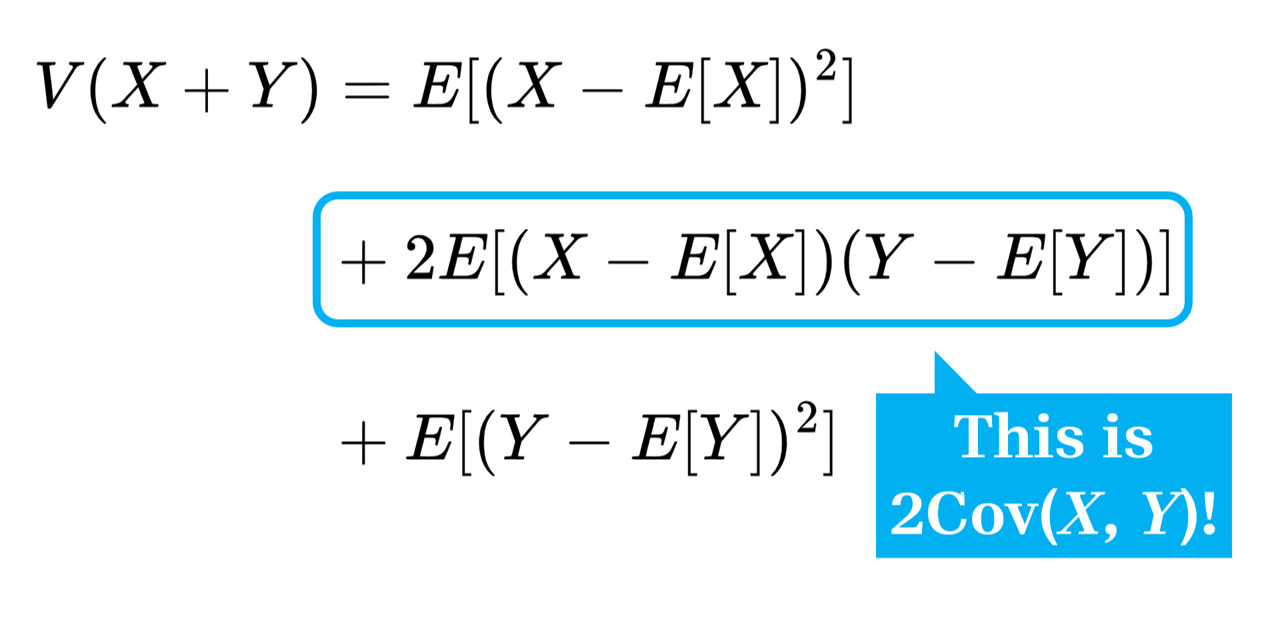The origin of 2ππ°π·(π, π ) in π(π + π )
The cross-product term in the square of a binomial expansion
For the variance of a sum of two random variables, I previously wrote that
\(V(X+Y) = V(X) + V(Y) + 2\text{Cov}(X, Y)\)
Where does the term 2Cov(X, Y) come from? Letβs dive into the mathematics.
If you re-write V(X+Y) according to its definition as an expected value, you will see that it is actually a binomial expansion with a power of 2.
\(\begin{align*}
V(X+Y) &= E\{[(X+Y)β(\mu_x+\mu_y)]^2\} \\
&= E\{[(Xβ\mu_x)+(Yβ\mu_y)]^2\}
\end{align*}\)
To make the notation easier to read, letβs use the following substitutions:
\(A = X-\mu_x\)
\(B = Y-\mu_y\)
Plugging A and B into that expectation,
\(\begin{align*}
V(X+Y) &= E[(A+B)^2] \\
&= E[A^2 + 2AB + B^2] \\
&= E(A^2) + 2E(AB) + E(B^2)
\end{align*}\)
Letβs now write that final line in terms of X and Y.
\(\begin{align*}
V(X+Y) &= E[(X-\mu_x)^2] + 2E[(X-\mu_x)(Y-\mu_y)] + E[(Y-\mu_y)^2] \\
&= V(X) + 2\text{Cov}(X,Y) + V(Y)
\end{align*}\)
As you can see, the covariance comes from the cross-product term in a binomial expansion.
