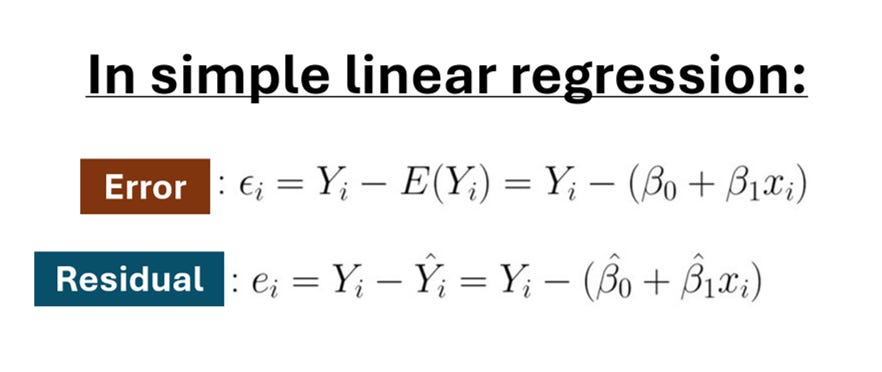Error vs. Residual in Simple Linear Regression

Separating the unobservable from the observable

In the context of linear regression, many data scientists seem to clump the terms “error” and “residual” together. This is wrong. They are actually 2 different (but related) concepts. Let’s explore them rigorously.

• The error is the difference between the observed response and the true value of the response. The error is a mathematical construct, and it is unknown.

• The residual is the difference between the observed response and the fitted response. The residual is known, and it is an estimate of the error for each particular value of the response variable.

\(\begin{align*} \text{Error} : \epsilon_i &= Y_i - E(Y_i) = Y_i - (\beta_0 + \beta_1 x_i) \\ \text{Residual} : e_i &= Y_i - \hat{Y}_i = Y_i - (\hat{\beta}_0 + \hat{\beta}_1 x_i) \end{align*}\)

If needed, I encourage you to review the model statement of linear regression in my previous article.

To learn more about residuals and how to analyze them, here is a relevant tutorial from Penn State Statistics. This tutorial uses the symbol

• “ϵ” for error

• “e” for residual

I have followed their nomenclature in my notation.