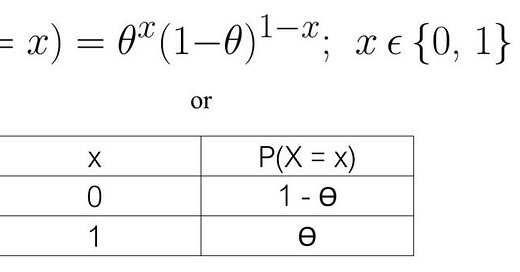The Bernoulli Distribution
A foundational concept in statistics and probability for binary outcomes
The Bernoulli distribution is a fundamental concept in probability and statistics. It is a discrete probability distribution that models a random variable with only 2 possible outcomes:
"success"1 (usually denoted by 1),
"failure" (usually denoted by 0).
An example is flipping a coin once; it can either land heads (success) or tails (failure).
This distribution is characterized by a single parameter, 𝛳, which represents the probability of success. Consequently, the probability of failure is 1 - 𝛳.
Returning to our example of flipping a coin, let’s assume that the coin is fair, so the probability of getting a heads or tails is the same.
The flip of a fair coin is a special case of the discrete uniform distribution. It has 2 categories (n = 2), and the probability for both categories is the same (1 ÷ 2 = 0.5).
You can show the probability mass function (PMF) of a Bernoulli random variable in 2 ways:
As a mathematical expression
As a table
The mathematical expression may look complicated, but it is fairly straightforward if you plug in each value of x. Try it, and you will see quickly that it is equivalent to the table.
The Bernoulli distribution has many practical applications; here are just a few of the common ones.
Customer acquisition: Will this client buy our product or not?
Quality control: Is a manufactured item defective or not?
Digital marketing: Did a visitor to our website click on an advertisement or not?
Loan approval: Should our bank approve or deny a loan application from a customer?
Spam detection: Does an email contain spam or not?
You may have heard of the binomial distribution; it is a generalization of the Bernoulli distribution. It models multiple Bernoulli random variables with the same success rate (𝛳), and I will write about it in a future article. Please stay tuned.
I put the words “success” and “failure” in quotation marks, because there is nothing inherently positive or negative about these outcomes. “Success” often denotes the outcome of interest, but it does not have to be a good or preferable outcome. In biostatistics, medicine, and clinical trials, statisticians sometimes use the Bernoulli distribution to describe a patient who may die of a certain disease. Death is a bad outcome, so it is not a success in the regular sense of the word, but it is the outcome that draws attention in this context.