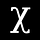Probability vs. Likelihood
The words "probability" and "likelihood" are interchangeable in everyday parlance; mathematically, their definitions even look the same. However, they actually mean very different things in statistics and probability. Let's use the example of coin flipping to illustrate their difference.
Probability measures the chance of an event occurring when there is uncertainty about the outcome. In the context of coin flipping, you can measure the chance of getting heads. Flip a coin 1,000 times, count the number of heads, and calculate1 the proportion of heads to get the probability.
On the other hand, likelihood measures how well a mathematical model explains the observed data. Rather than focusing on the event, likelihood is concerned with the parameter of the model that describes the underlying random process.
For instance, suppose that you flip a coin 1,000 times and get 573 heads.
You want to determine the fairness of the coin.
Mathematically, a fair coin has a Bernoulli distribution with a success parameter θ of 0.5.
Likelihood assesses how consistent this outcome (573 heads) is with θ = 0.5. A higher likelihood means more evidence that the observed outcome provides for the hypothesized probability.
To be specific in mathematical terms, you can formulate a likelihood function by
writing the joint probability density function (PDF) or probability mass function (PMF) of the random variables of interest,
declaring the distribution's parameter as the independent variable in the function.
This is shown in the image below. Notationally, the joint probability mass function and the likelihood look exactly the same. However, they mean different things and serve different purposes.
Here is a key difference between likelihood and probability: It is entirely possible for a likelihood to be greater than 1, but a probability is upper-bounded by 1.
In summary, probability is about predicting the future based on known frequencies, while likelihood is about interpreting observed data to infer the plausibility of various parameter values in a given mathematical model about the random nature of the event.
(There is a procedure called maximum-likelihood estimation, which finds the value of the parameter θ that maximizes the likelihood function; this value serves as a point estimate of θ. I will devote a separate post to discuss this topic in more detail.)
This implies the frequentist interpretation of probability. There is also the Bayesian interpretation of probability. For brevity, I am only mentioning frequentist probability in this article.